Дробь как одна или несколько равных дробей

У.: А что можно сказать о дробях и ?

Д.: >.

У.: Что можно сказать о дробях и ?.

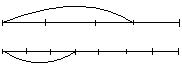
Д.: .

У.: А как сравнить дроби и ? Не можем же мы постоянно чертить отрезки и делить их? И неудобно это делить отрезок на 87 частей! Какую закономерность вы заметили?

Д.: больше та дробь, у которой знаменатель меньше.

Правило: Из двух дробей с одинаковыми числителями больше та, у которой знаменатель меньше, и меньше та, у которой знаменатель больше.

У.: Давайте посмотрим на такие пары дробей:

№2. а) и ; б) и ; в) и ?

У.: Что общего у этих пар дробей, чем похожи эти пары?

Д.: В каждой паре одна дробь правильная, другая – неправильная.

У.: Что можно сказать обо всех правильных дробях по отношению к единице?

Д.: Правильные дроби меньше единицы.

У.: А неправильные?

Д.: Неправильные дроби больше единицы.

У.: Какой напрашивается вывод?

Д.: Неправильная дробь больше правильной дроби.

У.: Расставим знаки сравнения:

№2. а) < ; б) > ; в) < .

Промежуточный итог:

Какие дроби мы научились сравнивать? (с одинаковыми знаменателя, с одинаковыми числителями, правильные и неправильные).

Закрепление материала – учащиеся работают у доски.

№3. Запишите дроби и сравните их.

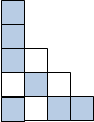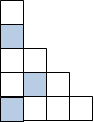а) и б) и

Историко-педагогическое исследование содержания педагогического образования в уездном городе Удмуртской Республики
На фоне происходящих перемен в системе педагогического образования актуальным становится обращение к историческому опыту. В связи с этим мы предприняли попытку обнаружить программы профессионального ...

Педагогический подход к содержанию и технологиям социальной работы с семьей
Современная семья сосредотачивает в себе всю совокупность социальных проблем свойственных современному обществу, образу жизни. Среди них можно выделить и собственно семейные проблемы. Это распределен ...