Математические развлечения

Домино - пасьянс:

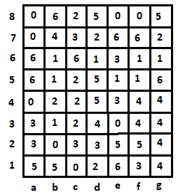
Цифровые узоры на диаграмме означают не что иное, как 28 косточек домино, уложенных в прямоугольник, состоящий из 56 (7 * 8) клеток. Каждая косточка домино занимает 2 клетки. Однако, границы косточек на рисунке не показаны. Их требуется восстановить, т.е. сгруппировать цифры (ограничить прямоугольниками) таким образом, чтобы в результате получился полный набор значений косточек домино от 0:0 до 6:6.

Для решения задач домино – пасьянс удобно выписывать все значения косточек домино вот такой «косынкой» и отмечать использованные клеточки:

0:0 1:1 2:2 3:3 4:4 5:5 6:6

0:1 1:2 2:3 3:4 4:5 5:6

0:2 1:3 2:4 3:5 4:6

0:3 1:4 2:5 3:6

0:4 1:5 2:6

0:5 1:6

0:6

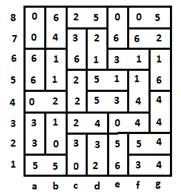
Рассмотрим приведенный пример.

Прежде всего отметим, что клетки b2, b3 может занять косточка 0:1 – другого такого сочетания, где бы рядом стояли 0 и 1, на поле нет. То же самое можно сказать и о косточках 2:4, 6:5. Они могут занять лишь клетки c3, d3 (2:4), e1, e2 (6:5).

Далее, как бы мы не расположили две косточки на клетках с1, с2, d1, d2, всегда при этом окажется, что клетка b1 окружена с трех сторон. Тем самым однозначно определили положение косточки 5:5 на а1, b1. При этом вновь оказывается, что клетка а2 окружена с трех сторон. Вследствие этого получаем 3:3 на а2, а3.

Косточка, занимающая клетку d2, может лечь двояко: на с2, d2 и на d1, d2. Но в первом случае определяется косточка 3:3, которая нами уже найдена (клетка а2, а3). Следовательно, косточка может занимать клетки d1, d2 и иметь значение 2:3. Теперь ясно, что клетки с1, с2 определяют косточку 0:3.

Обратим внимание на клетку е3. Эта клетка может входить в косточку 0:4 (e3, f3) или в косточку 0:3 (е3, е4). Положение последней уже определено, а поэтому заключаем: 0:4 занимает клетки e3, f3.

При этом сложится ситуация, аналогичная той, которая возникает при определении косточки 5:5. Дальнейший анализ показывает, что клетки g3, g4 занимает косточка 4:4, f1, g1 – косточка 3:4 и f2, g2 – косточка 5:4. Зная, что 3:4 определена, находим положение косточки 4:1 (f4, f5). Сразу видим, что клетки g5, g6 занимает косточка 6:1.

Далее, проведенные ранее рассуждения позволяют отыскать положение косточек 3:1 (е6, f6), 5:3 (в4, е4) и 5:1 (d5, е5). Косточка 6:1 выявлена, в силу этого находим, что косточка 1:2 занимает клетки d6, d7, а тогда косточка 2:5 – клетки с8, d8. Затем устанавливаем положение косточек 6:2 (f7, g7), 0:5 (f8, g8) и 6:0 (e7, e8). Из этого, что 6:0 найдена, следует 0:2 на а4, b4, а затем 2:2 на с4, с5.

Осталось определить положение пяти косточек: 0:0, 1:1, 4:6, 6:3 и 6:6. Но так как в оставшейся части поля цифры 0 и 1 встречаются только дважды, то ясно, что 0:0 будет на а7, а8, и 1:1 на b5, b6. А тогда определяются 6:6 (а5, а6), 6:3 (с6, с7) и 4:6 (b7, b8). Задача решена.

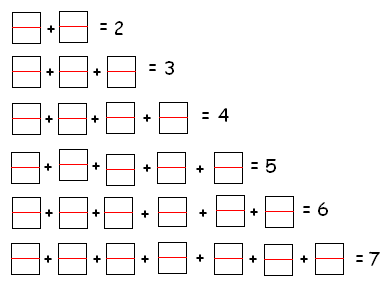
Домино «Дроби»:

Возьмите комплект домино и отложите в сторону кость 0:0. Теперь, рассматривая оставшиеся косточки как дроби (правильные и неправильные), расположите их как на рисунке, чтобы в каждой строке равнялась числу косточек данной строки.

Игровые головоломки

Кошки и собаки:

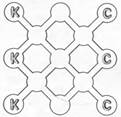
Три умные собаки и три хитрые кошки после обоюдоострых контактов оказались на противоположных площадках сквера и занялись решением очень важной для обеих сторон задачи: как им поменяться друг с другом местами, но при этом, чтобы не возникло новых потасовок, не только не встречаться друг с другом, но даже не оказываться на соседних площадках.

В результате была избрана следующая стратегия: собаки и кошки сидят на площадках, но время от времени либо кошка, либо собака бежит по аллее на соседнюю площадку. Кошки считают, что совместными усилиями за 32 перебежки (их и собачьи вместе) они смогут поменяться местами с собаками. Собаки с ними не согласны. Кто прав?

Формы работы социального педагога с детьми, оставшимися без попечения родителей
Форма – это то, благодаря чему какое – то явление существует для восприятия; это способ существования чего – либо; это плоть содержания. В «философской энциклопедии» понятие форма определяется так: « ...

Особенности эстетического воспитания
Наиболее интенсивное эстетическое развитие личности происходит в рамках школьного возраста. При этом для каждой возрастной группы учащихся характерны определенные этапы эстетического развития, связан ...