Математические развлечения

Первая цифра множимого 7 или 8; только эти две цифры дают цифру 7 в начале третьей строки при умножении множимого на 9. Используя это положение и то обстоятельство, что четвертая строка трехзначное число, делаем вывод: вторая цифра множителя равна 1.

При умножении на 1 число переписывается без изменения, а тогда число четвертой строки равно числу первой строки и третья цифра третьей строки есть 4.

Число третьей строки делится на 9. Используя признак делимости на 9, находим вторую цифру третьей строки как цифру, дополняющую сумму известных цифр до числа, кратного 9. Так как сумма известных цифр равна: 7+4+7=18, то в качестве неизвестной цифры может быть либо 0, либо 9. Итак, третья строка – 7047 или 7947, а множимое соответственно равно 783 или 883. Но при этом однозначно определилась вторая цифра множимого – 8, а следовательно, и вторая цифра четвертой строки тоже 8.

Четвертая цифра числа шестой строки определяется как последняя цифра суммы второй цифры числа третьей строки, второй цифры числа четвертой строки и четвертой цифры числа пятой строки. Пусть вторая цифра числа третьей строки равна 9. Тогда четвертая цифра числа пятой строки равна 0. Но это невозможно, так как в противном случае множитель начинался бы цифрой 0. Следовательно, вторая цифра числа третьей строки 0, то есть третья строка 7047, множимое примера – 783. Последняя цифра пятой строки 9. Это соответствует тому, что первая цифра множителя 3.

Итоги: 783×319=249777.

Ребусы с ключевыми словами

В этих ребусах предстоит расшифровать десятибуквенное ключевое слово, которое получиться, если расставите буквы соответственно ух числовому значению от 0 до 9. Разным цифрам соответствуют разные буквы. Между зашифрованными числами поставлены математические знаки, показывающие действия по горизонталям и по вертикалям. Путем рассуждений восстановите числовые значения букв так, чтобы выполнялись указанные действия.

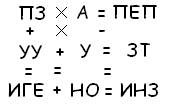
Рассмотрим сумму первого вертикального ряда ПЗ+УУ=ИГЕ. Сумма двух двузначных чисел не больше 198, а, следовательно, И=1.

Из равенства ПЕП – ЗГ =ИНЗ следует, что П = И +1, а поэтому П = 2.

В строке ИГЕ + НО = ИНЗ при сложении Г десятков с Н десяткам получается снова Н десятков. Это означает, что Г = 0(возможен случай Г = 9, но Г≠ 9, так как при сложении не происходит переноса единицы в разряд сотен).

Итак, Г = 0, И = 1, П = 2. А поэтому в равенстве ПЗ + УУ = ИГЕ У принимает значение 7 или 8. Пусть У = 8. В этом случае из равенства УУ + У = ЗТ вытекает, что Т = 6 и З = 9. Но тогда в разности ПЕП – ЗТ = ИНЗ получаем П = 5, а так как ранее установлено, что П = 2, то делаем вывод: У ≠ 8. Следовательно У = 7, тогда из УУ + У = ЗТ находим Т = 4, З = 8. Равенство ПЗ +УУ = ИГЕ при З = 8 и У = 7 дает Е = 5.

В сумме ИГЕ +НО = ИНЗ Е = 5, З = 8, а значит, тогда О = 3. В третьем вертикальном ряду известны значения всех букв, кроме одной – Н, поэтому значение этой буквы легко находится: Н = 6. И наконец, в равенстве А × У = Но получаем А = 9.

Ребусы с квадратиками

В ребусах этого раздела каждый квадратик означает какую либо цифру. Ни одно число в ребусах не равно нулю и не начинается цифрой нуль (однако на нуль числа могут оканчиваться).

Ребусы составлены так, что сумма чисел первого вертикального ряда равна результату, полученному от действий, произведенных над первой строкой, сумма чисел второго ряда одинакова с результатом второй строки, сумма чисел третьего вертикального ряда одинакова с результатом третьей строки и т.д.

Пример: В пустые квадратики поставьте соответствующие цифры, подобрав их так, чтобы, производя последовательно над числами в каждой строке ребуса указанные арифметические действия, можно было получить в результате то или иное число, стоящее после знака равенства.

Последовательно, - значит, так, как если бы каждая строка ребуса была снабжена скобками, показывающими последовательность арифметических действий:

Методы обучения в специальном детском саду
Особенности обучения детей дошкольного возраста При обучении детей с нарушениями зрения необходимо учитывать, что они развиваются по тем же самым законам, что и нормально видящие дети, но имеют свои ...

Понятие коллектива, структура коллектива. Влияние коллектива на личность
Термин «коллектив» произошел от латинского collektives- собирательный. Он означает социальную группу, объединенную на общественно-значимых целях, общественных ориентациях и совместной деятельности. К ...