В настоящее время около 30-40% детей испытывают трудности при обучении в школе. Наиболее остро этот вопрос встает на начальных этапах школьного обучения...
Игры в педагогическом процессе
Тема игры в педагогическом процессе очень актуальна, игра – мощнейшая сфера «самостоятельности» человека: самовыражения, самоопределения.
Свое название педагогика получила от греческого слова "пайдагогос" (пайд — дитя, гогос — веду), которое означает детоводство или дитяведение.
Способы получения поверхностей вращения второго порядка
3. 
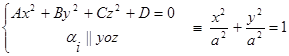- уравнение окружности
Исследуем уравнение I.
Пусть 
, D<0, A>0, B>0, C>0, тогда уравнение будет иметь следующий вид: 
, разделим это уравнение на 
получим уравнение: 
. Заменим: 
на 
, 
на 
, 
на 
, получим уравнение следующего вида: 
- это уравнение эллипсоида. Полученное уравнение может быть уравнением эллипсоида вращения при выполнении следующих условий:
При 
получим следующее уравнение: 
, при сечении данной поверхности второго порядка плоскостями параллельными координатной плоскости XOY в интервале - c<z<c получаются окружности.
При 
получим следующее уравнение: 
, при сечении данной поверхности второго порядка плоскостями параллельными координатной плоскости XOZ в интервале - b<y<b получим окружности.
При 
получим следующее уравнение: 
, при сечении данной поверхности второго порядка плоскостями параллельными координатной плоскости ZOY в интервале - a<x<a получим окружности.
При 
получим уравнение сферы, которое имеет вид: 
, при сечении данной поверхности второго порядка плоскостями параллельными координатным плоскостям XOY, XOZ, ZOY в интервале - c<z<c, - b<y<b,-a<x<a получим окружности.
При последующем приравнивании коэффициентов 
к нулю будем получать линии второго порядка:
,
,
.
Исследуем одно из уравнений:
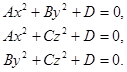
Пусть , D<0, A>0, B>0, тогда уравнение 
будет иметь следующий вид: 
, разделим это уравнение на получим уравнение: 
. Заменим: на , на , получим уравнение следующего вида: 
- это уравнение эллиптического цилиндра. Полученное уравнение может быть уравнением поверхности вращения второго порядка при выполнении следующего условия: , тогда получим следующее уравнение: 
, при сечении данной поверхности второго порядка плоскостями параллельными координатной плоскости XOY в интервале - c<z<c получим окружности.
Проблема общения и межличностные отношения в психологии
В социально-психологической литературе высказываются различные точки зрения на вопрос о том, где "расположены" межличностные отношения, прежде всего, относительно системы общественных отнош ...
Формы и методы социально-педагогической работы с беспризорниками
Социальная помощь детям в настоящее время – это социальное обслуживание и поддержка членов семьи, попавших в трудную жизненную ситуацию, оказании им комплекса социальных услуг и осуществление их соци ...
- Главная
- Коллектив как воспитательная система
- Процесс обучения
- Развитие памяти учащихся
- Физическое воспитание учеников
- Педагогика и воспитание
- Карта сайта
- Поиск