Способы получения поверхностей вращения второго порядка

Итак, при определенных значениях коэффициентов A, B, C, D уравнения , получаются уравнения следующих поверхностей вращения второго порядка:

- уравнение эллипсоида вращения,

- уравнение сферы,

- уравнение цилиндрической поверхности вращения,

- уравнение однополостного гиперболоида вращения,

- уравнение двуполостного гиперболоида вращения,

- уравнение конической поверхности вращения.

Исследуем одно из уравнений II

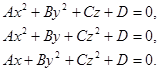
Пусть , A>0, B>0, C>0, тогда уравнение будет иметь следующий вид: , разделим это уравнение на получим уравнение: . Заменим: на , на , получим уравнение следующего вида: - это уравнение эллиптического параболоида. Полученное уравнение может быть уравнением поверхности вращения второго порядка при выполнении следующего условия: при , тогда получим следующее уравнение: , при сечении данной поверхности второго порядка плоскостями параллельными координатной плоскости XOY получим окружности.

Итак, при определенных значениях коэффициентов A, B, C, D уравнения , получаются уравнения следующих поверхностей вращения второго порядка: - уравнение эллиптического параболоида вращения.

Исследуем уравнения III:

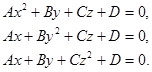
Уравнения представленные под цифрой IV не могут являться уравнениями поверхности вращения второго порядка, так как ни при каких значениях они не могут описывать поверхность вращения. В их параллельных сечениях не может получиться окружности, это связано с тем, что в данных уравнениях не хватает квадрата хотя бы ещё у одной переменной.

Домашнее чтение как вид речевой деятельности
Для более полного понимания домашнего чтения кратко рассмотрим основные виды чтения. Существует много различных классификаций видов чтения. В основу каждой из них кладутся разные принципы. Так, одни ...

Диагностика уровня реализации воспитательной функции в неполной семье младшего школьника
Повышенное внимание к семье со стороны всех социальных институтов на сегодняшний день объясняется процессами, происходящими в обществе – гуманизацией и демократизацией общественных отношений, ростом ...