Способы получения поверхностей вращения второго порядка

Геометрический способ

Пусть дана кривая l, которая лежит в плоскости XOY и имеет уравнение ; (рис.7). Найдём уравнение поверхности, которая получается при вращении кривой l вокруг оси ОХ (рис.8).

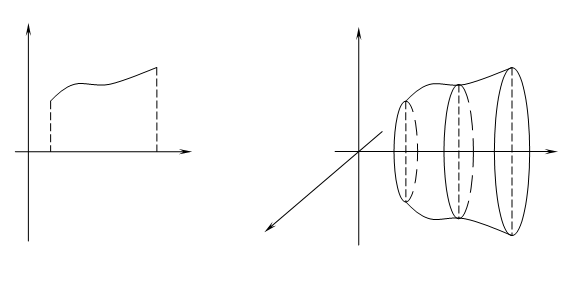
Очевидно, что точка М с координатами (x, y, z), где принадлежит искомой поверхности тогда и только тогда, когда , таким образом уравнение поверхности, полученной вращением кривой вокруг оси ОХ имеет вид: , . Это уравнение получено из уравнения кривой l следующим образом: обе части уравнения возводятся в квадрат и y2 заменяется на y2+ z2.

При вращении кривой или прямой вокруг одной из координатных осей можно получить поверхность вращения.

Для этого необходимо уравнение прямой или кривой сначала возвести в квадрат, а затем при их вращении вокруг оси OY x2 заменяется на x2+y2, при вращении вокруг оси ОХ y2 заменяется на y2+ z2.

Эллипсоид вращения

Поверхность, которая получается при вращении эллипса вокруг одной из осей, называется эллипсоидом вращения. Пусть в плоскости XOY эллипс задан уравнением: .

Составим уравнение поверхности, полученное вращением эллипса вокруг оси ОХ. Для этого в уравнении эллипса y2 заменим на y2+ z2. После замены получим: (I).

Это уравнение называется уравнением эллипсоида. При a >b уравнение (I) определяет эллипсоид вращения, вытянутый вдоль оси ОХ (приложение 1 рис.9), при a < b - эллипсоид вращения сжатый вдоль оси ОХ (приложение 1 рис.10), при a = b уравнение определяет сферу (приложение 1 рис.11).

Однополостный и двуполостный гиперболоиды вращения

Пусть в плоскости ХОУ дана гипербола, заданная уравнением . При вращении гиперболы вокруг одной из её осей получится поверхность вращения, называемая гиперболоидом вращения.

При вращении гиперболы вокруг её действительной оси (ОХ), получается двуполостный гиперболоид, чтобы получить его уравнение необходимо (достаточно) в уравнении гиперболы y2 заменяется на y2+ z2. После замены получим: . Двуполостный гиперболоид изображен в приложении 1 рис.12.

При вращении гиперболы вокруг её мнимой оси (ОУ), получается однополостный гиперболоид. Для получения уравнения поверхности однополостного гиперболоида нужно в уравнении гиперболы заменить x2 на x2+z2 после замены получим . Однополостный гиперболоид изображен в приложении 1 рис 13.

О тригонометрических функциях и о развитии тригонометрии
Индийские ученые положили начало учению о тригонометрических величинах, которые они рассматривали в пределах первой четверти круга. Синус и косинус встречаются в индийских астрономических сочинениях ...

Формирование позиции педагога-исследователя начальной школы в рамках образовательного модуля "методы педагогического исследования"
Глава посвящена изложению методов и приемов, позволяющих формировать у студентов позицию педагога-исследователя начальной школы в рамках образовательного модуля "Методы педагогического исследова ...