Способы получения поверхностей вращения второго порядка

Параболоид вращения

Поверхность которая получается при вращении параболы вокруг её оси симметрии называется параболоидом вращения. Пусть на плоскости ХОY парабола задана уравнением: . Параболоид можно вращать вокруг оси OY. При вращении параболы вокруг оси ОY необходимо заменить в уравнении x2 на x2+z2,, после замены получим уравнение: - это уравнение эллиптического параболоида, он изображен в приложении 1 рис.14.

Коническая поверхность

Поверхность которая получается при вращении прямой не параллельной осям координат называется конической. Пусть на плоскости ХОY прямая задана уравнением ky=x, где k коэффициент при y, возведем данное уравнение в квадрат получим: ky2=x2. При вращении данной прямой вокруг оси OY, заменим x2 на x2+z2 получим уравнение конуса: x2-ky2+z2=0 . Его изображение представлено в приложении 1 рис.15.

Цилиндрическая поверхность

Поверхность, которая получается при вращении прямой параллельной одной из осей координат, называется цилиндрической. Пусть на плоскости ХОY прямая параллельная оси OY задана уравнением , k число, возведём равенство в квадрат: при вращении данной прямой вокруг оси OY, заменим x2 на x2+z2 получим уравнение цилиндра: . Его изображение представлено в приложении 1 рис.16.

Аналитический способ

Общее уравнение поверхности второго порядка имеет вид: , где A/, G/, B/, M/, K/, C/, N/, T/, L/, D/ - коэффициенты.

В результате замены координат можно упростить уравнение. Поворотом осей координат можно добиться, чтобы уравнение поверхности не содержало слагаемого с произведением переменных xy, xz, yz. После поворота уравнение примет вид:

Для дальнейшего упрощения уравнения воспользуемся параллельным переносом. С помощью него можно добиться того, чтобы коэффициенты при x, y, z обратились в ноль, тогда уравнение примет следующий вид: - канонический вид уравнения поверхности второго порядка.

Итак, общее уравнение поверхности второго порядка в зависимости от значений коэффициентов A/, G/, B/, M/, K/, C/, N/, T/, L/, D/ и преобразованием плоскости можно привести к одному из видов:

.

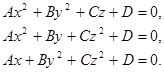
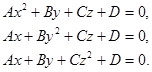
Для поверхности вращения второго порядка, расположенной в канонической системе координат, при её пересечении плоскостями, параллельными какой-либо координатной плоскости, должны получаться окружности, в таком случае исследование уравнения будет заключаться в том, чтобы определить при каких коэффициентах уравнение поверхности второго порядка будет отвечать хотя бы одному из условий:

1. 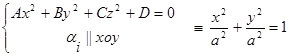- уравнение окружности

2. 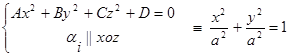- уравнение окружности

Методика и значение ознакомление дошкольников с родным городом
Известно, что дошкольный возраст – важнейший период становления личности, когда закладываются предпосылки гражданских качеств, развиваются представления детей о человеке, обществе и культуре. В.А.Сух ...

Контроль и учет знаний, умений и навыков учащихся по математике
Проверка и оценка знаний учащихся - необходимая составная часть процесса обучения математике. Контроль тесно связан с другими его звеньями - подачей нового материала, его закреплением, осознанием и п ...