Алгебраические числа

Определение. Если множество бесконечно и не является счетным, то оно называется несчетным.

Далее мы приведем примеры счетных и несчетных множеств, отметив пока, что рациональных чисел счетно, а действительных несчетно.

20. Примеры взаимно-однозначных соответствий.

Возьмем два отрезка равной длины. Соединим концы данных отрезков и увидим, что каждой точке одного отрезка соответствует точка другого:

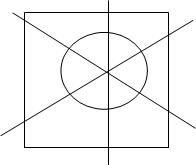
Как установить взаимно однозначное соответствие между окружностью и квадратом. Для этого достаточно вписать окружность в квадрат и проводить прямые через центр окружности до пересечения с квадратом. Тогда каждой точке окружности будет соответствовать точка квадрата.

Легко установить счетность множества Z целых чисел. Для этого расположим все целые числа таким образом: 0,1, - 1, 2, - 2,… Видно, что мы представили их в виде числовой последовательности вида a1, a2, a3, a4,… Можно было сделать иначе, указав номер N(x) целого числа x: 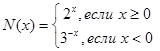. Правда при этом не каждое натуральное число будет номером какого-нибудь целого числа, например, уравнение N(x) = 5 не имеет решений, значит, 5 не является номером никакого целого числа.

По существу очевиден следующий результат.

Теорема. Бесконечное подмножество счетного множества счетно.

Из нее вытекает, что если каждому элементу множества удалось присвоить номер (при этом допустимо, что у некоторых элементов может оказать даже бесконечно много номеров), то это множество счетно.

С помощью этого замечания можно доказать, что рациональных чисел счетное число. Каждое рациональное число является отношением целых. Обозначим номер целого числа x через N(x), тогда можно присвоить номер рациональному числу x/y по формуле N(x/y) = 2N(x)3N(y). При этом каждому рациональному числу присваивается бесконечно много номеров ввиду неоднозначности представления рационального числа в виде дроби, однако разным рациональным числам присваиваются разные номера. При этом конечно есть натуральные числа (например, степени 5), которые не являются номером никакого рационального числа.

20. Свойства счетных множеств. Начнем со следующего простого факта.

Теорема. Пусть у нас есть счетные множества А, В, С. Тогда объединение этих множеств также счетно.

Доказательство. Так как все эти множества счетны, то они представимы в виде последовательностей: A: a1, a2, a3, …; B: b1, b2, b3, …; C: c1, c2, c3, … Объединение этих множеств содержит элементы каждого множества. Будем выписывать элементы объединения множеств, двигаясь по столбцам слева направо, а в каждом столбце сверху вниз: a1, b1, c1; a2, b2, c2; a3, b3, с3,…, т.е. объединение указанных множеств счетно. ÿ

Следующая теорема уже не столь очевидна.

Теорема 1. Счетное объединение счетных множеств счетно.

Доказательство. Запишем в виде таблицы элементы данных множеств, считая, что в первой строке занумерованы элементы первого множества и т.д. Рассмотрим систему расширяющихся квадратов Kn (n = 1, 2, …). Квадрат Kn находится на пересечении первых n строк и первых n столбцов таблицы. Теперь все элементы легко записать в виде последовательности. Сначала записываем элемент из первого квадрата, потом в любом порядке элементы второго квадрата (можно записанные ранее элементы не писать еще раз, а можно и писать), потом элементы третьего квадрата и т.д. ÿ

Условия организации опытно-практической работы
Опытно-практическую работу по организации проектной деятельности младших школьников на уроках технологии с использованием ИКТ мы проводили во время преддипломной педагогической практики в 4б классе с ...

Социально-мировоззренческие основы культуры Древнего Востока
История Древнего Востока ярко характеризует общие закономерности исторического процесса и те конкретные формы, в которых эти закономерности проявлялись в истории отдельных стран и народов. В целом ис ...