Алгебраические числа

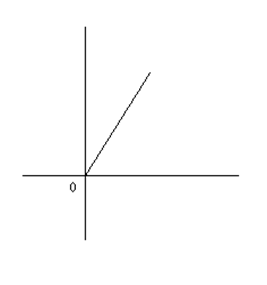
Проведем радиус-вектор в точку (a, b), пусть φ – угол между направлением оси 0x и данным радиус вектором, r – длина радиус-вектора.

Тогда число a + bi можем описать парой чисел (r, φ). При этом φ называется аргументом комплексного числа, а r – его модулем. Из прямоугольного треугольника имеем r2 = a2 + b2 (теорема Пифагора), значит, . Кроме того, используя понятия синуса и косинуса, получаем a = r cosφ, b = r sinφ. Тогда число z = a + bi представимо в виде: z = r (cosφ + sinφ). Указанное представление называется тригонометрической формой числа z. Отметим, что модуль числа находится однозначно, а аргумент с точностью до слагаемых вида 2pn, n – любое целое число.

40. Теорема Гаусса.

В множестве C комплексных чисел мы можем вычислить корень из отрицательного числа, и вообще корень любой натуральной степени. Всякое уравнение xn = z имеет ровно n корней. Более того, справедлива

Теорема Гаусса. Всякий многочлен n–ой степени с комплексными коэффициентами имеет ровно n комплексных корней.

В частности, можно разложить на множители сумму квадратов действительных чисел, правда, сомножители при этом оказываются комплексными:

a2 + b2 = (a + bi)(a – bi).

Определение. Числа a + bi и a - bi называются комплексно сопряженными.

При этом пишут . Перечислим свойства комплексного сопряжения:

; ; ; .

Гауссу принадлежит строгое определение понятия комплексного числа; он же предложил их изображать как точки на плоскости. Независимо от Гаусса идея геометрического представления комплексных чисел пришла к менее известным математикам – датчанину К.Весселю и швейцарцу Ж.Аргану. Обозначение мнимой единицы буквой i принадлежит Эйлеру.

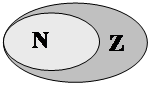
50. Расположение числовых систем. Изобразим рассмотренные выше числовые системы на диаграмме:

							Q		I
					R

Проблемы финансирования дошкольного образования в Российской Федерации
Проанализируем состояние системы дошкольного образования в Российской Федерации. Начиная с 1991г. (и по 2001г.) численность детей в дошкольных образовательных учреждениях сильно сократилась (с 8433 т ...

Проблемы воспитания в современной России
С социальными проблемами воспитания сталкиваются в любом обществе независимо от того, стабильное оно, не стабильное, переходное и т.д. Это могут быть самые разные социальные проблемы – от столь привы ...