Тождественные преобразования выражений и методика обучения учащихся их выполнению

Особую группу тождественных преобразований составляют тригонометрические выражения и логарифмические выражения.

К обязательным результатам обучения за курс алгебры в 7-9 классах относятся:

тождественные преобразования целых выражений

раскрытие скобок и заключение в скобки;

приведение подобных членов;

сложение, вычитание и умножение многочленов;

разложение многочленов на множители при помощи вынесения общего множителя за скобки и формул сокращённого умножения;

разложение квадратного трёхчлена на множители.

«Математика в школе» (Б.У.М.) стр.110

тождественные преобразования рациональных выражений: сложение, вычитание, умножение и деление дробей, а также применять перечисленные умения при выполнении несложных комбинированных преобразований.

учащиеся должны уметь выполнять преобразования несложных выражений, содержащих степени и корни.

Были рассмотрены основные типы задач, умение решать которых позволяют получить ученику положительную оценку.

Одной из самой важных сторон методики изучения тождественных преобразований является развитие учащимся целей выполнения тождественных преобразований.

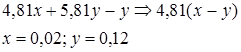- упрощение численного значения выражения

.

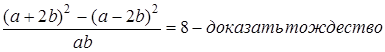какое из преобразований следует выполнить: (1) или (2) Разбор этих вариантов является мотивировкой (предпочтительнее (1), т.к. в (2) происходит сужение области определения)

Решить уравнение:

-разложение на множители при решении уравнений.

Вычислить:

Применим формулу сокращённого умножения:

(101-1) (101+1)=100102=102000

Найти значение выражения:

Для нахождения значения домножим каждую дробь на сопряжённый:

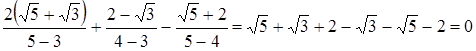
Построить график функции:

Выделим целую часть: .

Предупреждение ошибок при выполнении тождественных преобразований может быть получено путём варьирования примеров выполнения их. В этом случае отрабатываются «мелкие» приёмы которые как составные части входят в более объёмный процесс преобразования.

Например:

.

В зависимости от направлений уравнения можно рассмотреть несколько задач: справа налево умножение многочленов; слева направо -разложение на множители. Левая часть кратна одному из сомножителей в правой части и т.д.

Кроме варьирования примеров, можно воспользоваться проведением апологии между тождествами и числовыми равенствами.

Следующий приём – объяснение тождеств.

Для повышения интереса учащихся можно отнести отыскание различных способов решения задач.

Уроки по изучению тождественных преобразований станут интереснее, если их посвятить поиску решения задачи.

Например: 1) сократить дробь:

доказать формулу «сложного радикала»

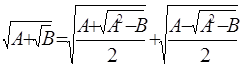
Рассмотрим:

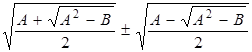
Преобразуем правую часть равенства:

-

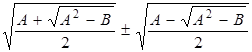сумма сопряжённых выражений. Их можно было бы домножить и разделить на сопряжённый, но такая операция приведет нас к дроби, знаменатель которой есть разность радикалов.

Сущность управления функционированием педагогической системы
Функционирующая школа – это школа, работающая в режиме традиционных форм, методов и средств организации учебно-воспитательного процесса и дающая, как правило, устойчивый стабильный результат. Инновац ...

Диагностика уровня реализации воспитательной функции в неполной семье младшего школьника
Повышенное внимание к семье со стороны всех социальных институтов на сегодняшний день объясняется процессами, происходящими в обществе – гуманизацией и демократизацией общественных отношений, ростом ...