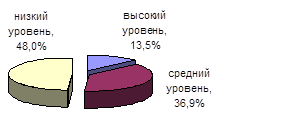В настоящее время около 30-40% детей испытывают трудности при обучении в школе. Наиболее остро этот вопрос встает на начальных этапах школьного обучения...

Игры в педагогическом процессе

Тема игры в педагогическом процессе очень актуальна, игра – мощнейшая сфера «самостоятельности» человека: самовыражения, самоопределения.

Предмет и функции педагогики

Свое название педагогика получила от греческого слова "пайдагогос" (пайд — дитя, гогос — веду), которое означает детоводство или дитяведение.

Интеграционные процессы в развитии системы высшего образования в Узбекистане

Педагогика и воспитание » Интеграционные процессы в развитии системы высшего образования в Узбекистане

Страница 15

что при k > 1 ни факторные нагрузки, ни сами факторы не определяются однозначно, т.к. в уравнении (*) факторы fj могут быть заменены любым ортогональным преобразованием.

Это свойство модели используется в целях преобразования (вращения) факторов, которое выбирается так, чтобы наблюдаемые величины имели бы максимально возможные нагрузки на один фактор и минимальные нагрузки на остальные факторы. Существуют различные практические способы оценки факторных нагрузок, имеющие смысл в предположении, что Xi, ., Xn подчиняются многомерному нормальному распределению с ковариационной матрицей С = {сij}.Выделяется максимального правдоподобия метод, который приводит к единственным оценкам для cij, но для оценок aij даёт уравнения, которым удовлетворяет бесчисленное множество решений, одинаково хороших по статистическим свойствам.

Вместе с тем, в работе использовался корреляционный анализ — метод обработки статистических данных, заключающийся в изучении коэффициентов (корреляции) между переменными. При этом сравнивались коэффициенты корреляции между одной парой или множеством пар признаков, для установления между ними статистических взаимосвязей. Корреляция отражала лишь линейную зависимость величин, но не отражала их функциональной связности. Например, при вычислении коэффициента корреляции между величинами A = sin(x) и B = cos(x), он был близок к нулю, т.е. зависимость между величинами отсутствовала. Между тем, величины A и B были связаны между собой функционально по закону sin^2(x) + cos^2(x) = 1.

В обработке сигналов использовалась автокорреляционная функция (АКФ), которая определялась интегралом и ваимнокорреляционная функция (ВКФ).

Корреляция отражала лишь линейную зависимость величин, но не отражала их функциональной связности. Например, вычисление коэффициента корреляции между величинами A = sin(x) и B = cos(x), будет близок к нулю, т.е. зависимость между величинами отсутствует. Между тем, величины A и B очевидно связаны функционально по закону sin^2(x) + cos^2(x) = 1.

Измерение профессиональных интересов связано, преимущественно, с решением практических задач и индивидуального планирования самостоятельной работы студентов-бакалавров в процессе их подготовки к прохождению педагогической практики в школах, лицеях и колледжах города Ташкента. Такая подготовка носит личностно-ориентированный, эмпирический характер. Необходимо отметить, что при подготовке был осуществлен факторный анализ оценок теста профессиональных интересов, а также интеркорреляция между шкалами – показателями различных годов проведенных срезов.

Таблица 1.

Статистические показатели параметров по индикаторам факторного и интеркорреляционного анализа (ИФИА) по основным характеристикам профессиональных склонностей у студентов экспериментальной (ЭГ) и контрольной групп (КГ)

По профессиональному мышлению	Средний показатель подготовки		По научно-исследовательской компетенции		Средний показатель подготовки		По профессионально-ситуативной компетенции	Средний показатель подготовки
По профессиональному мышлению	ЭГ	КГ	По научно-исследовательской компетенции		ЭГ	КГ	По профессионально-ситуативной компетенции	ЭГ	КГ
выводы	3,61	3,08	определение цели исследования		3,70	2,74	стабильного интереса к решению задач (мотивации)	3,63	2,51
индуктивные обобщения	3,51	3,1	обоснованность метода исследования		3,48	2,38	формулировка темы, к которой относится задача	3,47	2,71
дедуктивные обобщения	3,68	3,01	актуализации необходимых знаний		3,33	2,46	выделения когнитивных задач темы	3,34	2,49
объяснения актуальности выбора	3,30	2,69	формулирование и обоснование гипотезы		3,19	2,22	применения теоретических знаний	3,28	2,31
допустимые ошибки	3,07	2,37	презентация результатов исследования		3,41	2,49	профессионального объяснения решения задачи	3,06	2,33
доказательства и факты	2,92	2,23					самооценка реализованного задания	3,84	2,83
Средние показатели ИФИА основополагающих характеристик профессионального мышления:
профессионально-логического мышления	3,35	2,74	овладения профессионально - исследовательским методом		3,41	2,47	решения профессионально-ситуативных задач	3,44	2,55
Уровень интегрального специально-предметного показателя профессионального мышления								3,39	2,58
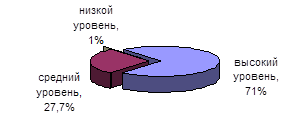
Рис 1. Ранжирование студентов экспериментальной группы по шкалам ИФИА профессионального мышления на начальном диагностическом этапе				Рис 2. Ранжирование студентов экспериментальной группы по шкалам ИФИА профессионального мышления на итоговом диагностическом этапе
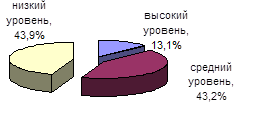
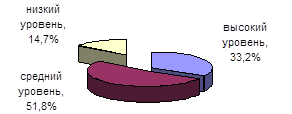
Рис 3. Ранжирование студентов контрольной группы по шкалам профессионального мышления на начальном диагностическом этапе				Рис 4. Ранжирование студентов контрольной группы по шкалам ИФИА профессионального мышления на итоговом диагностическом этапе

Страницы: 10 11 12 13 14 15 16 17 18 19 20

Нюансы образования:

Использование нетрадиционных приемов обучения рисованию животных
Особенностью преподавания изобразительного искусства является то, что издавна соперничают два основных подхода, которые можно определить как академическое обучение и свободное воспитание. В первом сл ...

Познавательный интерес как психолого-педагогическая проблема
Проблема интереса в обучении не нова. Значение его утверждали многие дидакты прошлого. В самых разнообразных трактовках проблемы в классической педагогике главную функцию его видели в том, чтобы приб ...

Категории