Развивающее обучение решению математических задач

На современном этапе образования под развивающим обучением понимается обучение младших школьников общим приемам умственной деятельности, а на уроках математики – общим приемам по усвоению математических понятий (наблюдению, анализу, сравнению, заключению по аналогии, абстрагированию, синтезу, обобщению, дедуктивному, индуктивному умозаключению, классификации и др.)

Мы рассмотрим некоторые методические вопросы обучения детей общим приемам решения любых математических задач. Эти приемы учебной деятельности можно представить в виде схемы:

Схема. "Приемы учебной деятельности "

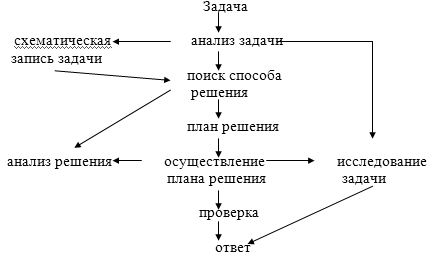
рис.1

В настоящее время далеко не каждого ребенка удается научить решать математические задачи. Основная причина заключается в том, что младшие школьники, прочитав задачу, не анализируют ее, а сразу приступают к решению, не обосновывая выбор арифметического знака действия.

Как научить ребенка сначала приступать к анализу задачи, составлению плана решения и только потом к ее решению.

Сначала следует научить ребенка читать задачу, понимать смысл прочитанного, пересказывать содержание, подмечать, какие события произошли в задаче: что было, что изменилось, что стало; объяснить, что обозначает каждое число в задаче, в чем суть тех или других математических выражений. В этом плане интересен опыт польской школы, в котором значительное учебное время отводится на рассмотрение так называемых "задач без вопросов". При таком методическом подходе дети приобретают первые навыки анализа условия задачи на основе событий, происходящих в задаче. Далее дети учатся правильно ставить вопрос к условию задачи (или составлять по вопросу условие задачи), выделять в задаче условие и ее вопрос. Нетрудно заметить, что на этом этапе начинается обучение детей составлению, сочинению, придумыванию задач, что может стать основным методическим приемом в практической учителя.

Путь к осознанному решению задач лежит главным образом через составление их детьми. Опытные учителя начальной школы делают это по картинкам; числовым данным; вопросу; дополнению задач не достающими данными или вопросом; решению или ответу; схеме, чертежу, краткой записи; плану решения; формулам; данным, взятым из справочников, таблиц и т. д.

Такая творческая работа приводит к составлению сборников задач, придуманных учениками класса.

Обучение анализу задачи на этом не заканчивается, а исследование ее продолжается при иллюстрации задачи рисунками, схемами, чертежами, при записывание краткого условия задачи.

В этом случае учебные действия согласно теории поэтапного формирования (А. Н. Леонтьева, П. Я. Гальперина) осуществляются при работе с материальными или материализованными объектами и проговариваются вслух (громкое проговаривание) с постепенным переходом к умственной форме действий (проговаривание про себя – в "уме").

Обратимся снова к нашей схеме исследования задачи – к выбору способа решения задачи. К сожалению, в начальной школе в настоящее время практически отсутствует на уроках математики алгебраический и геометрический способы решения задачи, а преобладает в основном арифметический, да и только в виде решения задач по действиям. Поэтому дети весьма ограничены в плане выбора способа решения – они решают задачи по действиям или составляют математическое выражение, хотя в программе по математике и есть решение простейших уравнений, но это проходит пропедевтической нитью через решение задач за все годы начального обучения математике. У многих младших школьников так и не сформировано представление о том, что задачи могут решаться алгебраическим или геометрическим способами. Отсюда напрашивается вывод о возвращении к методическим идеям шестидесятых годов, когда в учебниках математики довольно в полном объеме были реализованы вопросы алгебраической и геометрической пропедевтики. Наверное, уже в 1 классе целесообразно при решение задач на нахождение неизвестного слагаемого показать детям на уровне первичных преставлений, что данную задачу можно решить и с помощью уравнения, не вводя, естественно, это умение в ранг обязательных требований.

Диагностика уровня сформированности познавательной активности у детей старшего дошкольного возраста
Опытно-экспериментальная часть работы проводилась на базе МДОУ «Детский сад № 85 комбинированного вида» г. Саранска. В эксперименте приняли участие дети старшей группы в количестве 24 человек. Они бы ...

Характеристика универсальной учебной деятельности
Последовательная реализация деятельностного подхода направлена на повышение эффективности образования, более гибкое и прочное усвоение знаний учащимися, возможность их самостоятельного движения в изу ...