Приемы устного счета. Китайский алгоритм

«Китайский» алгоритм умножения трехзначных чисел, имеющий популярность на сайте Youtube, основан на законе дистрибутивности операции умножения, относительно операции сложения:

(100а+10b+c)·(100e+10f+h)=

10000ae+1000af+100ah+1000be+100bf+10bh+100ce+10cf+ch=

10000ae+1000(af+be)+100(ah+bf+ce)+10(bh+cf)+ch

Покажем, как работает этот алгоритм на примере умножения 123 и 241.

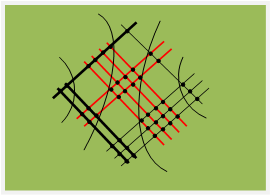
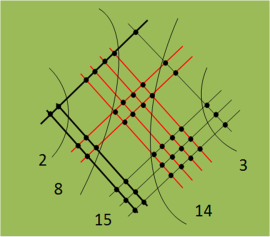
20000 + 8000 + 1500 + 140 + 3 = 20000 + 8000 + (1000 + 500) + (100 + 40) + 3

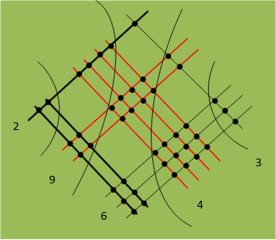
20000 + 9000 + 600 + 40 + 3 = 29643

Умножение на однозначное число

Умножение на 4.

Чтобы устно умножить число а на 4, его дважды удваивают.

Обоснование: а·4=а·2·2.

Например:

122·4=244·2=488

335·4=670·2=1340

Умножение на 5.

Чтобы устно умножить число на 5, его умножают на 10 и делят на 2, то есть приписывают к числу 0 и делят пополам.

Обоснование: а·5=а·10:2.

Например:

74·5=74·10=740:2=370

243·5=243·10=2430:2=1215

При умножении числа на 5 четного числа 2а, проще сначала делить число пополам, а затем умножить результат на 10.

Обоснование: 2а·5=2а:2·10=а·10.

Например:

74:2·10=37·10=370

Умножение на 6.

Чтобы умножить число на 6 его умножают на 5 и прибавляют множимое. Как мы уже знаем, чтобы умножить число на 5 его умножают на 10 и делят на 2.

Обоснование: а·6=а·(5+1)=а·10:2+а.

Например:

36·6=36·5+36=36:2·10+36=180+36=216

164·6=164·5+164=164:2·10+164=820+164=984

Умножение на 8.

Чтобы умножить число на 8, его трижды удваивают.

Обоснование: а·8=а·2·2·2=2а·2·2=4а·2

Например:

37·8=74·4=148·2=296

217·8=434·4=868·2=1736

Умножение на 9.

Чтобы умножить число на 9, умножают его на 10 и отнимают множимое.

Обоснование: а·9=а·(10–1)=10а–а.

Например:

89·9=89·10–89=801

375·9=375·10–375=3375

Умножение на двузначное число

Умножение на 11.

Чтобы устно умножить число на 11, его умножают на 10 и прибавляют множимое.

Обоснование: а·11=а·(10+1)=10а+а.

Например:

87·11=87·10+87=870+87=956

645·11=6450+645=7095

Умножение на 15.

Чтобы устно умножить число на 15, его умножают на 1,5 (случай рассматривается ниже) и умножают на 10.

Обоснование: а·15=а·1,5·10=1,5а·10.

Например:

18·15=18·1,5·10=270

45·15=45·1,5·10=675

Умножение на 25.

Чтобы устно умножить число на 25, его умножают на 100 и делят на 4.

Обоснование: а·25=а·100:4=100а:4.

Например:

74·25=74·100:4=7400:4=1850

484·25=48400:4=12100

Умножение на 50.

Чтобы устно умножить число на 50, его умножают на 100 и делят на 2.

Обоснование: а·50=а·100:2=100а:2.

При умножении числа на 50 четного числа 2а, проще сначала делить число пополам, а затем умножить результат на 100.

Например:

46·50=46:2·100=23·100=2300

847·50=847·100=84700:2=42350

Умножение на 99.

Чтобы устно умножить число на 99, его умножают на 100 и отнимают множимое.

Обоснование: а·99=а·(100–1)=100а–а.

Например:

46·99=46·100=4600–46=4554

745·99=745·100=74500–745=73755

Умножение на дробные числа

Умножение на 1 ½.

Чтобы устно умножить число на 1 ½, прибавляют к множимому его половину.

Обоснование: а·1 ½ = а·1+ а· ½

Например:

34·1 ½=34·1+34·½=34+17=51

23·1 ½=23·1+23·½=23+11,5=34,5

Умножение на 1 ¼.

Чтобы устно умножить число на 1 ¼, прибавляют к множимому его четверть.

Обоснование: а·1 ¼ = а·1+а· ¼

Например:

48·1 ¼=48·1+48· ¼=48+12=60

56·1 ¼=56·1+56· ¼=56+14=70

Умножение на 2 ½.

Примерная структура занятия по лыжной подготовке
Вводно-подготовительная часть Общая задача: организация группы для предстоящих занятий и подготовка занимающихся к последующей более интенсивной нагрузке. Частные задачи: 1) организовать группу для з ...

Деятельностно-профессиональная подготовка учителя технологии в процессе педагогического образования.
С давних времен умение шить считалось как мужским занятием, так и женским. И если простейшую штопку носков и пришивание воротничков мужчины отвергали категорически, то высокое искусство творить моду ...