Основные типы поверхностей второго порядка и их свойства

Эллипсоид

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, c > 0, называется эллипсоидом. Эллипсоид изображен на рисунке 1.

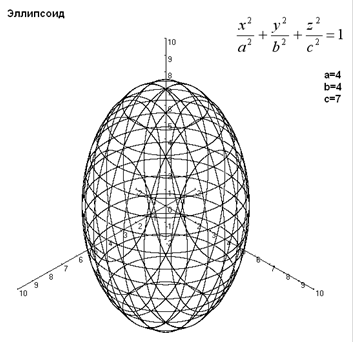
Рис.1

Свойства эллипсоида

Эллипсоид - ограниченная поверхность, поскольку из его уравнения следует, что

Эллипсоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно координатных осей,

плоскостной симметрией относительно начала координат.

В сечении эллипсоида плоскостью, перпендикулярной любой из координатных осей, получается эллипс.

Эллиптический параболоид

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, называется эллиптическим параболоидом. Эллиптический параболоид изображен на рисунке 2.

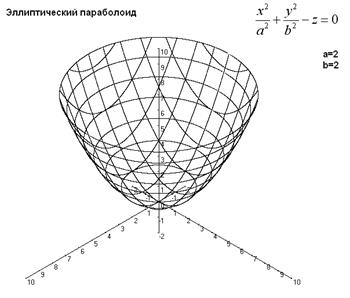
Рис.2

Свойства эллиптического параболоида

Эллиптический параболоид - неограниченная поверхность, поскольку из его уравнения следует, что z ≥ 0 и принимает сколь угодно большие значения.

Эллиптический параболоид обладает

осевой симметрией относительно оси Oz,

плоскостной симметрией относительно координатных осей Oxz и Oyz.

В сечении эллиптического параболоида плоскостью, ортогональной оси Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy - парабола.

Однополостный гиперболоид

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, c > 0, называется однополостным гиперболоидом. Однополостный гиперболоид изображен на рисунке 3.

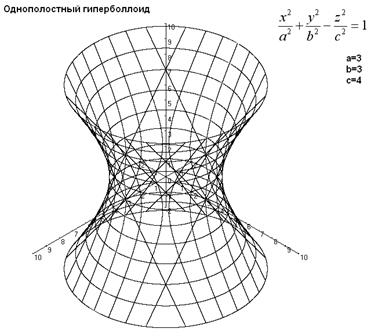
Рис.3

Свойства однополостного гиперболоида

Однополостный гиперболоид - неограниченная поверхность, поскольку из его уравнения следует, что z - любое число.

Однополостный гиперболоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, получается эллипс, а плоскостями, ортогональными осям Ox и Oy - гипербола.

Двуполостный гиперболоид

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, c > 0, называется двуполостным гиперболоидом.

Двуполостный гиперболоид изображен на рисунке 4.

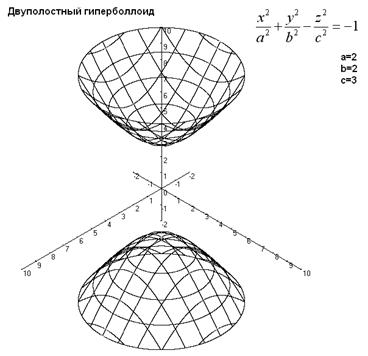
Рис.4

Свойства двуполостного гиперболоида

Двуполостный гиперболоид - неограниченная поверхность, поскольку из его уравнения следует, что

Двуполостный гиперболоид обладает

центральной симметрией относительно начала координат,

осевой симметрией относительно всех координатных осей,

плоскостной симметрией относительно всех координатных плоскостей.

В сечении однополостного гиперболоида плоскостью, перпендикулярной оси координат Oz, при |z|>c получается эллипс, при |z|=c - точка, а в сечении плоскостями, перпендикулярными осям Ox и Oy, - гипербола.

Коническая поверхность

Поверхность, задаваемая в некоторой прямоугольной декартовой системе координат уравнением , a > 0, b > 0, c > 0, называется конической поверхностью. Коническая поверхность изображена на рисунке 5.

Методы и приемы словарной работы с детьми раннего возраста
Словарная работа в каждой группе проводится на основе учета возрастных и индивидуальных особенностей словаря, психического развития в целом, а также текущих воспитательных задач. Методы и приемы слов ...

Методологические аспекты развития человека в физкультурном пространстве
Полипредметный анализ литературных источников показал, что современное естествознание постулирует объективность развития человека, в том числе и в процессе занятий физической культурой и спортом. Пос ...